Advanced Scripting: 02 Koch Snowflake

Course or Collection:

Advanced C# Scripting in Grasshopper

Software:

C# / Grasshopper / Rhino

Tag:

Scripting

Video Duration:

7 minutes

Author:

Zach Downey

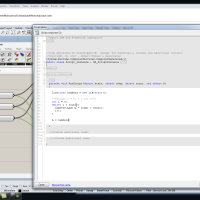
In this tutorial we create a Koch Snowflake. To do it, we create two methods, CreateTri and CreateKochSnowflake. This component as a boolean toggle to invert the snowflake. It works by reversing the polyline direction. It's kinda cool. Check out the video and the code.

//Create an empty list of lines to hold our snowflake curves
    List<Line> lines = new List<Line>();
    //Call the CreateTri function and pass the radius and flip parameters
    Polyline tri = CreateTri(radius, flip);
    //Create an array of Lines by extracting the segements from the triangle
    Line[] triangle = tri.GetSegments();
    //Add these three lines to the lines List
    lines.Add(triangle[0]);
    lines.Add(triangle[1]);
    lines.Add(triangle[2]);
    //Create a temporary list of lines
    List<Line> tempList = new List<Line>();
    //Begin the while loop
    int i = 0;
    while(i < num){
      //make sure the list is empty by calling the Clear() method
      tempList.Clear();
      tempList.AddRange(lines);
      lines.Clear();
      lines.AddRange(CreateKochSnowflake(tempList));
      i++;
    }
    A = lines;
  }

public List<Line> CreateKochSnowflake(List<Line> lines){
    List<Line> newLines = new List<Line>();
    foreach( Line ln in lines){
      //Get the length of the line and 4 points to define new snowflake edge
      double tempLength = ln.Length;
      Point3d ptStarttemp = ln.PointAt(0.0);
      Point3d pt1temp = ln.PointAt(0.333);
      Point3d pt2temp = ln.PointAt(0.666);
      Point3d ptEndtemp = ln.PointAt(1.0);
      //Create a new line and rotate it by 60 degs or PI/3
      Line rotatedLine = new Line(pt1temp, pt2temp);
      rotatedLine.Transform(Rhino.Geometry.Transform.Rotation(Math.PI / 3, pt1temp));
      //Create a new point from the end of the rotatedLine and complete the lines
      Point3d triTop = rotatedLine.PointAt(1.0);
      Line completeTriLine = new Line(triTop, pt2temp);
      Line lnStart = new Line(ptStarttemp, pt1temp);
      Line lnEnd = new Line(pt2temp, ptEndtemp);
      //Add all of the lines to the newLines list in order
      newLines.Add(lnStart);
      newLines.Add(rotatedLine);
      newLines.Add(completeTriLine);
      newLines.Add(lnEnd);
    }
    return newLines;
  }

public Polyline CreateTri(double radius, bool reverseTri)
  {
    List<Point3d> pts = new List<Point3d>();
 
    //Angles for triangle points
    const double ang0 = (Math.PI / 2);
    const double ang1 = (7 * Math.PI / 6);
    const double ang2 = (11 * Math.PI / 6);
    //Create the three points of the triangle
    Point3d pt0 = new Point3d(radius * Math.Cos(ang0), radius * Math.Sin(ang0), 0);
    Point3d pt1 = new Point3d(radius * Math.Cos(ang1), radius * Math.Sin(ang1), 0);
    Point3d pt2 = new Point3d(radius * Math.Cos(ang2), radius * Math.Sin(ang2), 0);
    //Add the points to the pts list
    pts.Add(pt0);
    pts.Add(pt1);
    pts.Add(pt2);
    //Create a new polyline called pl
    Polyline pl = new Polyline();
    //loop through the list of points(should only be three but will use any number b/c we aren't checking BAD!)
    foreach(Point3d pt in pts){
      pl.Add(pt);
    }
    //Add a copy of the first point to the end of the list to close the polyline
    pl.Add(pts[0]);
    //Check to see if the polyline should be reversed and if true...call the reverse method
    if(reverseTri == true){
      pl.Reverse();
    }
    return pl;
  }