Intro to Python Scripting: 23 Recursion Koch Curve
Course or Collection:
Tag:
Video Duration:
20 minutes
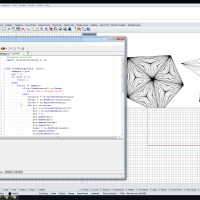
In this tutorial we once again take a look at recursion. This time we look at creating the Koch Curve using recursion. This is similar to the C# version I did for the Advanced GH Scripting. In this case we only do it for a line, instead of a polyline but for the most part the logic is similar.
#Koch Snowflake in python using recursion import rhinoscriptsyntax as rs #get normal/perpendicular vector def getnormal(pt1,pt2): dx = pt2[0] - pt1[0] dy = pt2[1] - pt1[1] return [-dy,dx,0] #split line recursive function def splitlines(lines, count): #temp list and clear input list templines = lines lines = [] #make sure we have a way to break the recursion if count == 0: return 1 else: for line in templines: #get properties of the line (endpts, length, direction, domain) stpt = rs.CurveStartPoint(line) endpt = rs.CurveEndPoint(line) length = rs.Distance(stpt, endpt) dir1 = rs.VectorCreate(endpt,stpt) crvdomain = rs.CurveDomain(line) #parameters for midpt and pts 1/3 and 2/3 along the line t0 = crvdomain[1] / 2.0 t1 = crvdomain[1] / 3.0 t2 = t1*2 midpt = rs.EvaluateCurve(line, t0) ptatonethird = rs.EvaluateCurve(line, t1) ptattwothird = rs.EvaluateCurve(line, t2) midpt = rs.AddPoint(midpt) #call get normal function normal = getnormal(stpt,endpt) #move midpt perpendicular to line at 1/3 the length of the line scaled = rs.VectorScale(normal,0.3333) rs.MoveObject(midpt,scaled) #create the 4 newlines and add them to the list newline1 = rs.AddLine(stpt, ptatonethird) newline2 = rs.AddLine(ptatonethird, midpt) newline3 = rs.AddLine(midpt, ptattwothird) newline4 = rs.AddLine(ptattwothird, endpt) lines.append(newline1) lines.append(newline2) lines.append(newline3) lines.append(newline4) #create a list of objects to delete cleanup = [] cleanup.append(line) cleanup.append(midpt) rs.DeleteObjects(cleanup) #don't forget to decrement the count otherwise infinite loop count = count - 1 return splitlines(lines,count) lines = [] # get two points to start count = rs.GetInteger("How many iterations would you like to do?", 3) pt1 = rs.GetPoint("Pick a start point") pt2 = rs.GetPoint("Pick an end point") line = rs.AddLine(pt1,pt2) lines.append(line) splitlines(lines,count)
Want to Contribute?
Want to be an author? Drop us a line here we'd love to have you.
Already have a video you'd like to post? Send us a link and we'll get you going.
:)

Comments
Jean-Jacques replied on Permalink